Extracting the trend of a time series is an important
analytical task as it simply depicts the underlying movement of the variable of
interest. Had this so-called long term component known in advance, we would
have been able to foresee its future course. In practice, however, there are
several other factors (e.g. cycle, noise) in play that have influence on the
dynamics of a time dependent variable.
Time path of a variable can either be deterministic
(assuming the change in trend is constant) or stochastic (assuming the change
in trend varies randomly around a constant). Estimation of a deterministic
trend is straightforward, yet it often oversimplifies the data generating
process. The assumption of stochastic trend seems to be a better fit to
observed behavior of various time series as they tend to evolve with abrupt
changes. Nevertheless, its estimation is difficult and can have serious
implications due to accumulation of past errors.
Kim et.al. (2009) proposed l1 trend filtering method, which produces trend
estimates that are piecewise linear. In this method, changes in slope of the
estimated trend can also be interpreted as abrupt changes or events in the
underlying dynamics of the time series in question.
EViews add-in "l1filter" implements the primal-dual
interior point method1 outlined in Kim et.al. (2009). The add-in is designed to work in series object and
can also be run from command line. In that respect, it is similar to “hpfilter1s”
add-in. For details, please see the information in the documentation that comes
with the add-in.
l1 trend filtering method can also be
thought of as a segmented linear regression, where we fit a straight line on
each segment. Note that this is different than the approach of breakpoint
regression as the latter does not necessarily have consistent values at the
join points.
The use of add-in is demonstrated below on a different data
set than that of Kim et.al. (2009) in order to avoid slow computing time2.
Instead, a low frequency macroeconomic time series data is chosen for the
purpose: Monthly Industrial Production Index (2010=100) of Turkish Economy
between January 1986 and August 20163.
Import the data into EViews4:
import .\tripi.xls
range=mevsim_1986!$B$5:$N$37 byrow colhead=1 namepos=all na="#N/A" names=(, , , , , , , , , , , , ,
, , , , , , , , , , , , , , , , 2013, 2014, 2015, 2016) @freq U 1 @smpl @all
Restructure the workfile:
pagestack num? @
*? *
pagestruct(freq=m,
start=1986, end=2016)
Get rid of unnecessary series:
delete id01 series01
var01 year
Change the name of dependent variable:
rename num ipitr_adj
Plot the series:
ipitr_adj.line
Estimate a deterministic trend:
equation eqdet.ls ipitr_adj c @trend
Visualize the fit:
eqdet.resids
Estimate a stochastic trend (i.e. Hodrick-Prescott filter5):
freeze(graph_hp) ipitr_adj.hpf(lambda=14400) trend_hp
Estimate l1
trend:
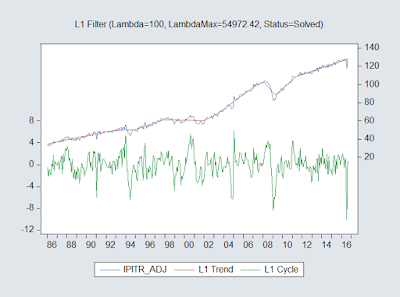
Ipitr_adj.l1filter(trend=trend_l1,lambda=100,draw)
We can compare two estimated trends:
graph graph_comp.line trend_hp trend_l1
graph_comp.draw(shade, bottom) 2008m01 2010m12 'shade the period of interest
Please note the relatively smooth transition behavior of
HP filter around the global financial crisis of 2008 and the V-shaped recovery
pattern captured (more accurately) by l1 filter.
l1 trend is also more robust to
end-point sensitivity:
smpl @first 2016m07 'drop the last observation
ipitr_adj.hpf(lambda=14400) trend_hpb
ipitr_adj.l1filter(trend=trend_l1b,lambda=100)
line trend_l1-trend_l1b trend_hp-trend-hpb
smpl @all
Another useful practical application of l1 filter is the identification of breakpoints
(i.e. kink points) for a given time series as it has the ability to estimate
piecewise linear trend, where the consecutive segments have consistent values
at their join points. EViews already allows breakpoint estimation, which does
not require such consistency when used in the identification of breaks for the
time series of interest. Although Bai and Perron (2003) make some
very useful and practical recommendations, deciding the number and type of
breaks is still an art as much as a science. In this case, global maximization
approaches seem to work better as they are able to identify important turning
points more successfully (with a margin of error, of course) in the history of
Turkish economy6:
equation eqbreak.breakls(method=globplus1,trim=5,size=1,heterr)
ipitr_adj c @trend
string breaks = eqbreak.@breaks 'save the dates of breakpoints
Visualize the fit:
eqbreak.resids(g)
Save the fitted values:
eqbreak.fit trend_break
We can compare the results from both analyses:
line trend_break trend_l1
l1 filtering is a
useful tool for both trend estimation and breakpoint detection of a time
series. Although the add-in can only be used for such purposes only, the
interior-point method developed by authors can be extended to handle the
problems in areas like; univariate time series decomposition, outlier
detection, regularized least squares, multivariate time series analysis, etc.
References
1 Please visit authors’ web page for details: http://web.stanford.edu/~boyd/papers/l1_trend_filter.html
2 The original algorithm exploits the sparse matrix structure, which EViews does not have that functionality (yet).
3 Officially adjusted for calendar and seasonal effects: http://www.turkstat.gov.tr/PreTablo.do?alt_id=1024
4 You can download the data from: http://www.turkstat.gov.tr/PreIstatistikTablo.do?istab_id=2418
5 In order to reflect the usual practice in macroeconomic time series modelling, default value of HP filter is preferred here (Hodrick and Prescott, 1997). In the original study, however, authors used the same lambda for both L1 and HP filters. Difference in the results would become much more pronounced if we did so.
6 Turkey experienced major economic crises of domestic nature in 1994 and 2001. Asian crisis hit Turkish economy during 1998 and not to mention the impact from global financial crisis of 2008. As of end-2010, Central Bank of Turkey announced a new (unconventional) monetary policy for the sake of financial stability and introduced the interest rate corridor framework from 2011 and onwards.
Bai, J. and Perron, P. (2003). "Computation and Analysis
of Multiple Structural Change Models", Journal
of Applied Econometrics, v. 18, pp. 1–22.
Hodrick, R. J. and Prescott, E. C. (1997). "Postwar U.S.
Business Cycles: An Empirical Investigation", Journal of Money, Credit and Banking, Vol. 29, pp. 1-16.
Kim, S-J., Koh, K., Boyd, S. and Gorinevsky, D. (2009). "L1 Trend Filtering", SIAM Review, Vol. 51(2), pp. 339-360.
1 Please visit authors’ web page for details: http://web.stanford.edu/~boyd/papers/l1_trend_filter.html
2 The original algorithm exploits the sparse matrix structure, which EViews does not have that functionality (yet).
3 Officially adjusted for calendar and seasonal effects: http://www.turkstat.gov.tr/PreTablo.do?alt_id=1024
4 You can download the data from: http://www.turkstat.gov.tr/PreIstatistikTablo.do?istab_id=2418
5 In order to reflect the usual practice in macroeconomic time series modelling, default value of HP filter is preferred here (Hodrick and Prescott, 1997). In the original study, however, authors used the same lambda for both L1 and HP filters. Difference in the results would become much more pronounced if we did so.
6 Turkey experienced major economic crises of domestic nature in 1994 and 2001. Asian crisis hit Turkish economy during 1998 and not to mention the impact from global financial crisis of 2008. As of end-2010, Central Bank of Turkey announced a new (unconventional) monetary policy for the sake of financial stability and introduced the interest rate corridor framework from 2011 and onwards.
No comments:
Post a Comment